The main parameter is the sun position and besides, the equation should be capable of characterizing the overall collector efficiency in a manner compatible to the experimental evaluation of its capabilities, with respect to the energy yield of the concentrating system. In the figures below, a vertical cross-section of the receiver is presented, showing the path of the incident rays along with the main geometric dimensions involved in the optical and thermal modeling (left picture). Besides, the heat fluxes, to and from the working fluid are schematically depicted (right picture), which determine the behavior and the efficiency of the collector. More specifically, the distribution of the incident radiative heat flux along the perimeter of the absorbing surface is shown (in red), along with the heat losses to the environment.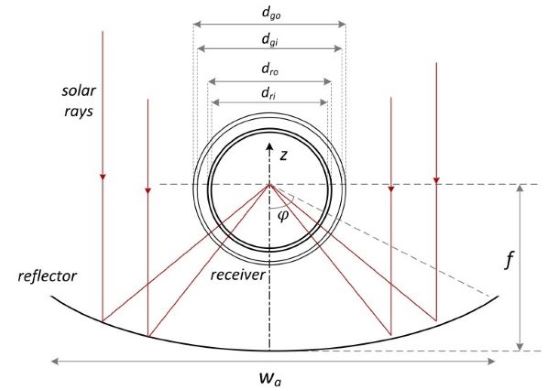
Besides heat losses, losses at the end of the collector are accounted for in the model (by means of a receiver length loss of lendl, as shown in the picture below), as well as those due to the variation in the incidence angle of solar radiation. The present investigation, more specifically, assumes that the collector losses can be expressed by an equation of the following form :
This equation, apart from thermal losses represented by the last three terms, includes also the end losses of the reflecting surface by means of a coefficient nendl in the first term, along with an incidence angle coefficient kb.
The objective of this investigation is the search for suitable coefficients α1, α2 … by comparisons with experimental data, so that in the future this equation can be employed for an accurate estimation of the losses and, consequently, the efficiency of the collector by making use of quantities that can be easily measured during its operation.